12. 常微分方程式

12.1 概要

常微分方程式 (ODE) は科学技術計算においてはしばしば現れます. 解析的に解けることが少なく, 数値解法に頼ることが多くなります.

12.1.1 初期値問題

1 階の常微分方程式は次のように表されます.
\[
y’ = \frac{dy}{dt} = f(t, y)
\] ここで, \(y\) は \(t\) の未知の関数 \(y(t)\) です. 常微分方程式の初期値問題は, 初期点 \(t = t_0\) における関数値 \(y = y_0 = y(t_0)\) (初期条件とよばれます) が与えられたとき, 最終点 \(t_f\) における関数値 \(y(t_f)\) を求めることを初期値問題といいます.

12.1.2 1 階の連立方程式

1 階の常微分方程式の初期値問題は, スカラー \(y\) をベクトル \(\boldsymbol{y}\) に代えてこのまま連立方程式に拡張することができます.
\[
\boldsymbol{y’} = \boldsymbol{f}(\boldsymbol{y}, t) \\
\boldsymbol{y_0} = \boldsymbol{y}(t_0) \\
\] 例えば, 2 変数の場合についてスカラー式に書き下すと次のようになります.
\[
y_1′ = f_1(y_1, y_2, t) \\
y_2′ = f_2(y_1, y_2, t) \\
\] スカラーの初期条件は 2 つ必要で, 次のようになります.
\[
{y_1}_0 = y_1(t_0) \\
{y_2}_0 = y_2(t_0) \\
\]

12.1.3 高階の常微分方程式

高階の常微分方程式, すなわち, 2 階以上の微分を含んだ常微分方程式は, 1 階の連立常微分方程式の形にして扱うこともできます. 例えば, 次の微分方程式を考えます.
\[
y” = f(y, y’, t)
\] これは, \(y_1 = y, y_2 = y’\) とおけば, 次のように 1 階の連立常微分方程式にすることができます.
\[
y_1′ = y_2 \\
y_2′ = f(y_1, y_2, t) \\
\] この場合には次のように 2 つの初期条件が必要になります.
\[
y_1(t_0) = y(t_0) = y_0 \\
y_2(t_0) = y'(t_0) = y’_0 \\
\] 同様にして 3 階以上の連立常微分方程式を解くこともできます.

12.2 常微分方程式の初期値問題の解法

12.2.1 オイラー法

変数 \(t\) を離散化して, \(t_0, t_1, \dots , t_n, \dots\) と表します. これらの点の間隔をステップ幅といい, \(h_n\) で表します.
\[
h_n = t_{n+1} – t_n
\] ステップ幅は必ずしも一定でなくてもよいのですが, ここでは \(n\) によらず一定にすることにして単に \(h\) と表します. 未知関数 \(y(t)\) の \(t_n\) における値 \(y(t_n)\) の近似値を \(y_n\) と表します.

ここで, 微分を差分近似すると次のように表されます.
\[
y’_n = f(t_n, y_n) \simeq (y_{n+1} – y_n) / h
\] これより次の近似式が得られます.
\[
y_{n+1} = y_n + hf(t_n, y_n)
\] この式を使って初期値 \(y_0\) から始めて, \(y_1, y_2, \dots\) と次々に各点における近似解を求める方法をオイラー法といいます.

オイラー法の式は \(y\) をテイラー展開したときに 2 次以上の項を省略したものに相当するので 1 次の解法と呼ばれ, 誤差は \(h^2\) のオーダー (\(O(h^2)\)) になります.

12.2.2 ルンゲ・クッタ法

ルンゲ・クッタ法は \(f()\) の微分を計算することなく高次のテイラー展開に相当する精度を得る方法です. いくつかの \(t\) と \(y\) について \(f(t, y)\) を計算し, それらの重み付き平均を作ってテイラー展開の \(p\) 次の項まで一致させることにより \(p\) 次の公式を作ります.

ルンゲ・クッタ法の一般形は次のようになります.
\[
\begin{align}
& y_{n+1} = y_n + h\sum_{i=1}^s b_ik_i \\
& k_i = f(t_n + c_ih, y_n + h\sum_{j=1}^s a_{ij}k_j) \\
\end{align}
\] \(a_{ij}, b_i, c_i\) はパラメータです. ここでは \(a_{ij} = 0 (j >= i), c_i = \sum_{j=1}^s a_{ij}\) とします. なお, \(s\) は段数と呼ばれます.

12.2.2.1 ホイン法

\(s = 2\) の場合, テイラー展開式の 2 次の項まで一致するようにできて次式が成り立ちます.
\[
\begin{align}
& b_1 + b_2 = 1 \\
& b_2c_2 = 1/2 \\
& b_2a_{21} = 1/2 \\
\end{align}
\] 未知数が 4 個で式が 3 本なので自由度が 1 あります. よく使われるものとしては, \(c_2 = 1\) とした次式をホイン法といいます. 通常は 2 次のルンゲ・クッタ法とは呼びません.
\[
\begin{align}
& y_{n+1} = y_n + h(k_1 + k_2)/2 \\
& k_1 = f(t_n, y_n) \\
& k_2 = f(t_n + h, y_n + hk_1) \\
\end{align}
\] これは 2 次の公式で, 誤差は \(O(h^3)\) になります.

12.2.2.2 4 次のルンゲ・クッタ法

\(s = 4\) の場合, 4 次の公式を作ることができます. この場合, パラメータは 12 個で式が 8 本なので自由度が 4 になり, 多様な公式を作ることができます. 最もよく使われているのは次式です.
\[
\begin{align}
& y_{n+1} = y_n + h(k_1 + 2k_2 + 2k_3 + k_4)/6 \\
& k_1 = f(t_n, y_n) \\
& k_2 = f(t_n + h/2, y_n + hk_1/2) \\
& k_3 = f(t_n + h/2, y_n + hk_2/2) \\
& k_4 = f(t_n + h, y_n + hk_3) \\
\end{align}
\] これは, 単にルンゲ・クッタ法と呼ばれることが多い 4 次の公式で, 誤差は \(O(h^5)\) になります.

12.2.3 埋め込み型ルンゲ・クッタ法

ここまで示した解法の誤差は \(O(h^p)\) なので \(h\) を小さくするほど精度が上がります. しかし, \(h\) を小さくするほど目的の解を求めるまでの \(f()\) の計算回数が増えるというトレードオフの関係にあります.

もし, 得られた結果の精度を知ることができれば, 要求精度に対して適切な(必要十分な)ステップ幅 \(h\) を選ぶことができ無駄な計算時間を費やさなくてよくなります.

そこで, 解を求めるだけではなく誤差の推定も効率よく行える公式が開発されています. 埋め込み型ルンゲ・クッタ法は 1 つの公式で 2 つの異なった次数の近似解を求めることができるものです. 次数の高い方の解は計算結果として, もう一つは誤差推定のために使われます.

これを使うと推定誤差をもとにステップ幅 \(h\) を自動的に調節しながら解を求める「適応プログラム」を作ることができます.

例として, 埋め込み型ルンゲ・クッタ法の公式である 5(4)次 ルンゲ・クッタ・フェールベルグ法の公式を下に示します. これを使った適応プログラム RKF45 は古くから広く使われています.
\[
\begin{align}
& y_{n+1} = y_n + h((16/135)k_1 + (6656/12825)k_3 + (28561/56430)k_4 – (9/50)k_5 + (2/55)k_6) \space (計算用: 5次の公式) \\
& y^*_{n+1} = y_n + h((25/216)k_1 + (1408/2565)k_3 + (2197/4104)k_4 – (1/5)k_5) \space (誤差評価用: 4次の公式) \\
& k_1 = f(t_n, y_n) \\
& k_2 = f(t_n + (1/4)h, y_n + (1/4)hk_1) \\
& k_3 = f(t_n + (3/8)h, y_n + (1/32)h(3k_1 + 9k_2)) \\
& k_4 = f(t_n + (12/13)h, y_n + (1/2197)h(1932k_1 – 7200k_2 + 7296k_3)) \\
& k_5 = f(t_n + h, y_n + h((439/216)k_1 – 8k_2 + (3680/513)k_3 – (845/4104)k_4)) \\
& k_6 = f(t_n + (1/2)h, y_n + h((-8/27)k_1 + 2k_2 – (3544/2565)k_3 + (1859/4104)k_4 – (11/40)k_5)) \\
\end{align}
\] 計算用には 5 次の公式を使います. \(h\) の自動調節は誤差評価用の 4 次の公式との差 \(\delta_{n+1} = ||y_{n+1} – y^*_{n+1}||\) の値を使って行います.

12.2.4 各解法の比較

上に説明した各解法により計算を行ってみます.

例題 1

次の初期値問題を解く.
\[
\frac{dy}{dt} = 1/(2 – t)^2 \space (y(0) = 0.5)
\] この例題は代数的に解を求めることができ, 次のようになります.
\[
y = 1/(2 – t)
\] 下図では横軸に誤差 (右に行くほど精度がよい), 縦軸に計算量 (= 関数呼び出し回数 (\(f(t, y)\) を何回呼び出したか)) を対数目盛りで示します. グラフが右下にいくほど性能がよいことになります.

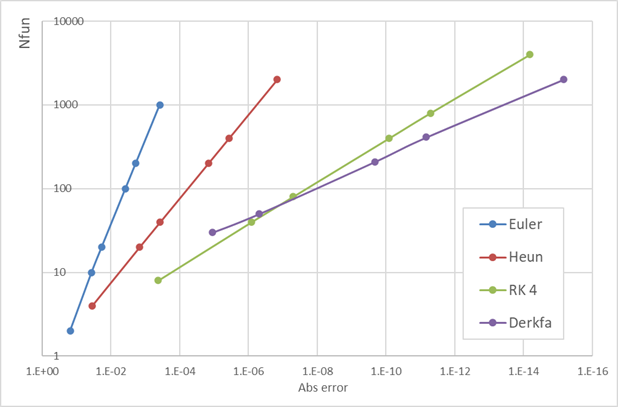
オイラー法は 1 次, ホイン法は 2 次, ルンゲ・クッタ法は 4 次の公式です. それぞれは (対数プロットで) 直線関係を示しますが, 傾きが次数を反映しています.

Derkfa は XLPack で使われている 5(4)次 ルンゲ・クッタ・フェールベルグ法の適応プログラムです. \(h\) の自動調節のためのオーバーヘッドがあるため純粋な 5 次の公式よりはやや効率が悪くなります.

12.2.5 2 階の常微分方程式

2 階の常微分方程式で次のような特別な形が現れることがよくあります.
\[
y” = f(y, t) \space (y’ に依存しない)
\] 2 階の常微分方程式は 1 階の連立常微分方程式の形にして解くことができると説明しましたが, このような特別な形の場合には 2 階のまま直接解く公式, 例えばニュストレム法が開発されています.

12.3 XLPack を使った常微分方程式の解き方

Derkfa は 5(4)次ルンゲ・クッタ・フェールベルグ法による適応プログラムで, RKF45 とほぼ同じものですが密出力機能 (後述) を追加しています.

Dopn43 は 4(3)次ルンゲ・クッタ・ニュストレム法による適応プログラムです. \(y’\) に依存しない特別な形の 2 階連立常微分方程式に使用します.

Derkfa および Dopn43 は XLPack ソルバーから使うこともできます.

12.3.1 単一の常微分方程式

単一の (連立ではない) 常微分方程式の例を例題 1 を使って説明します.

12.3.1.1 VBA プログラムを使用した解き方 (1)

Derkfa を使ったプログラム例を示します.

Const Ndata = 19, RowR = 5, ColR = 1
Dim Neval As Long

Sub F(N As Long, T As Double, Y() As Double, Yp() As Double)
    Yp(0) = 1 / (2 - T) ^ 2
    Neval = Neval + 1
End Sub

Sub Start()
    Const N = 1
    Dim Y(N - 1) As Double, T As Double, Tout As Double, Tend As Double
    Dim RTol(0) As Double, ATol(0) As Double
    Dim Mode As Long, Info As Long, I As Long
    RTol(0) = 0.00000001 '** 1.0e-8
    ATol(0) = RTol(0)
    Mode = 2
    T = Cells(RowR, ColR)
    Y(0) = Cells(RowR, ColR + 1)
    Tend = Cells(RowR + Ndata, ColR)
    Info = 0
    For I = 1 To Ndata
        Tout = Cells(RowR + I, ColR)
        Neval = 0
        Call Derkfa(N, AddressOf F, T, Y(), Tout, Tend, RTol(), ATol(), Mode, Info)
        If Info <> 0 And Info <> Mode Then
            Cells(RowR + I, ColR + 2) = "Error: " + Str(Info)
            Exit For
        End If
        Cells(RowR + I, ColR + 1) = Y(0)
        Cells(RowR + I, ColR + 2) = Neval
    Next
End Sub

Derkfa は目標精度を与えるとステップ幅を自動的に調節して解を求めます. 微分方程式をサブルーチン F として用意し, 初期値と要求精度を指定して呼び出すと解 (\(y\) の値) を求ることができます.

この場合, 連立方程式ではないので Y() と Yp() は配列ではなくて単純な変数でよさそうですが, VBA の引数の整合性のために配列で宣言して Y(0) と Yp(0) のみを使用します.

Mode = 2 は通常の動作モードで, T の初期値から始めて最終値 Tend まで計算を行います. ステップ幅は要求精度に合わせて最適になるように自動的に調節されます. 途中 Tout が最適ステップ幅よりも近くにきたら, 次のステップがちょうど Tout にくるようにステップ幅を変更してから計算し途中経過を返すために戻ります. その後 Tout を再設定して再呼び出しすることにより Tend までの計算を継続します.

Neval は関数評価回数をカウントするためだけの変数です.

このプログラムを実行すると, 次の結果が得られました.

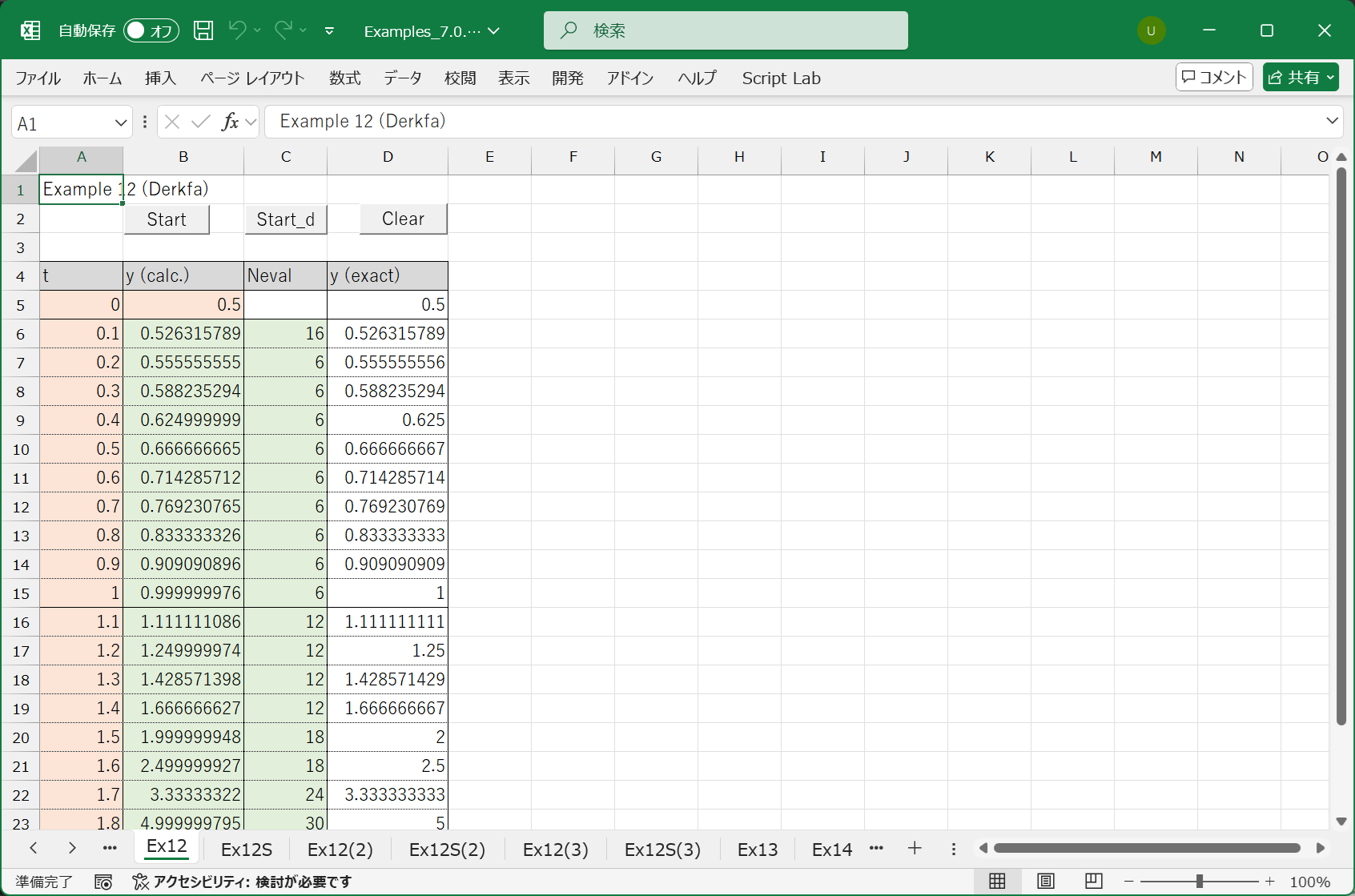
要求精度の 8 桁で正しい結果が得られています. なお, スタート直後と \(t\) が大きくなり変化が急になってきたときに, 精度を保つために関数評価回数が増えている(ステップ幅を小さくした)のがわかります.

12.3.1.2 VBA プログラムを使用した解き方 (2)

リバースコミュニケーション版 (RCI) の Derkfa_r を使ったプログラム例を示します.

Sub Start_r()
    Const N = 1
    Dim Y(N - 1) As Double, T As Double, Tout As Double, Tend As Double
    Dim RTol(0) As Double, ATol(0) As Double
    Dim Mode As Long, Info As Long, I As Long
    Dim TT As Double, YY(0) As Double, YYp(0) As Double, IRev As Long
    RTol(0) = 0.00000001 '** 1.0e-8
    ATol(0) = RTol(0)
    Mode = 2
    T = Cells(RowR, ColR)
    Y(0) = Cells(RowR, ColR + 1)
    Tend = Cells(RowR + Ndata, ColR)
    Info = 0
    For I = 1 To Ndata
        Tout = Cells(RowR + I, ColR)
        Neval = 0
        IRev = 0
        Do
            Call Derkfa_r(N, T, Y(), Tout, Tend, RTol(), ATol(), Mode, Info, TT, YY(), YYp(), IRev)
            If IRev = 1 Then
                YYp(0) = 1 / (2 - TT) ^ 2
                Neval = Neval + 1
            End If
        Loop While IRev <> 0
        If Info <> 0 And Info <> Mode Then
            Cells(RowR + I, ColR + 2) = "Error: " + Str(Info)
            Exit For
        End If
        Cells(RowR + I, ColR + 1) = Y(0)
        Cells(RowR + I, ColR + 2) = Neval
    Next
End Sub

目的関数を外部サブルーチンとして与えるのではなく, IRev = 1 のときに TT および YY の値を使って関数値を計算し YYp() に入れて再度 Derkfa_r を呼び出します. RCI の詳細については こちら を参照してください.

このプログラムを実行すると上と同じ結果が得られます.

12.3.1.3 VBA プログラムを使用した解き方 (3)

Derkfa による密出力機能を使った例を示します. 密出力機能とは, 途中経過出力のために戻るときにステップ幅の変更を行わず, 最適ステップ幅をキープしてトータルの関数評価回数を減らす機能です. 途中経過の解は補間により求められます.

注 – 密出力について詳しくは こちら を参照してください(目次の下の中央付近の「密出力」タブをクリックしてください).

密出力機能を使用するためにはプログラムにおいて Mode = 2 の代わりに Mode = 3 とするだけです. 12.3.1.1 のプログラムで Mode = 3 と変更したものを実行すると次の結果が得られました.

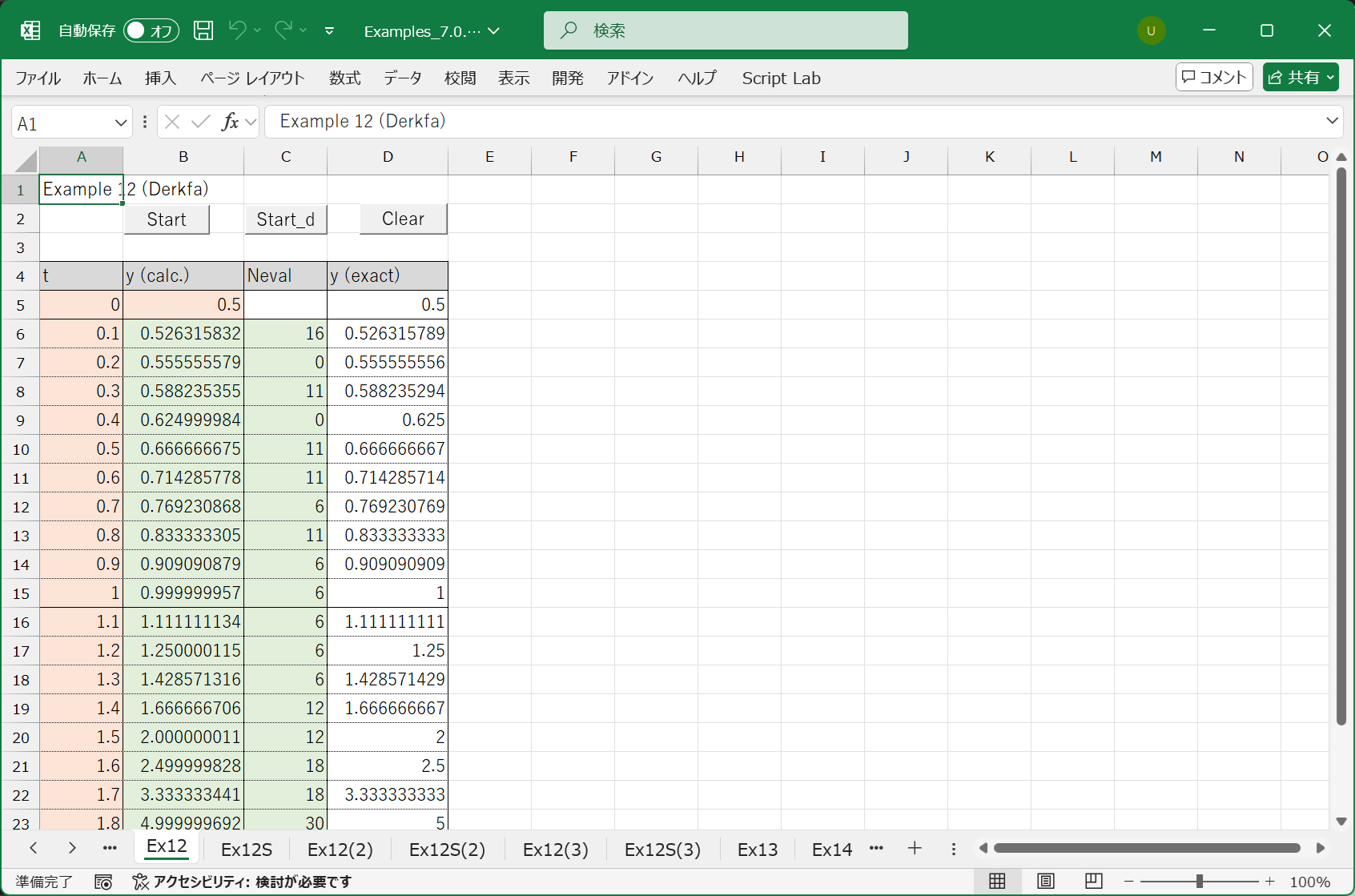
関数評価回数 Neval = 0 の区間がありますが, こういうところでは補間により解を求めていることがはっきりとわかります.

密出力機能は, 例えば滑らかなグラフを描くためなど, 要求精度が高くはないが途中経過の出力間隔を狭くしたい場合などに効果を発揮します.

12.3.1.4 ソルバーを使用した解き方

XLPack ソルバーアドインの「1 階常微分方程式」を使って解くこともできます. B6セルに数式 (=1/(2-B4)^2) が入力されています.

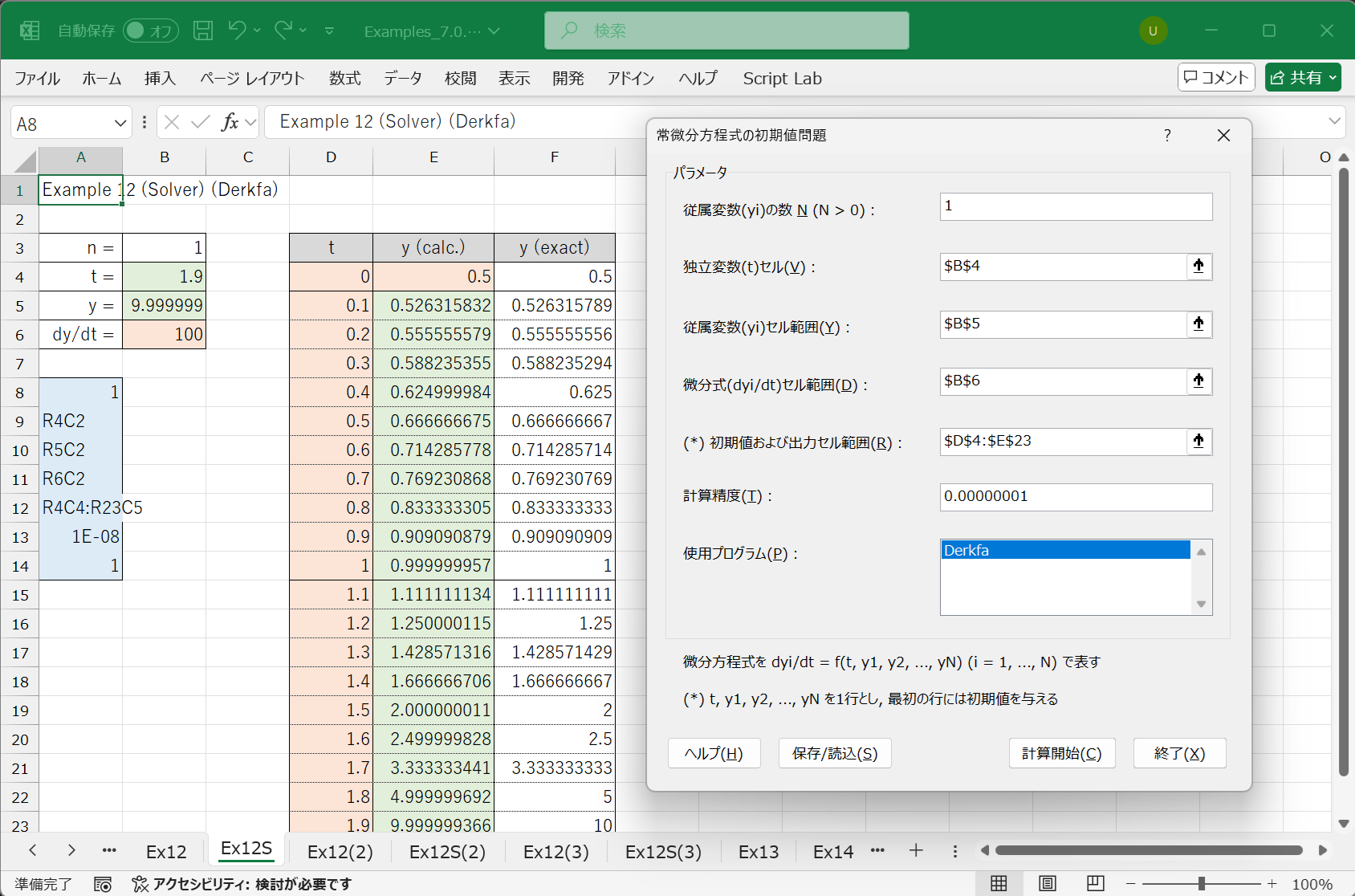
ソルバーについては こちら も参照ください.

12.3.2 連立常微分方程式

連立常微分方程式の例を説明します.

例題 2

次の初期値問題を解け.
\[
\frac{d^2y1}{dt^2} = -y1/r \\
\frac{d^2y2}{dt^2} = -y2/r \\
\] ただし,
\[
r = (y1^2 + y2^2)^{3/2} \\
\] \(t = 0\) において,
\[
y_1 = 1, y_2 = 0, dy_1/dt = 0, dy_2/dt = \sqrt{3}
\]

12.3.2.1 VBA プログラムを使用した解き方 (1)

この例題は 2 元連立方程式ですが, Derkfa を使って解くためには 12.1.3 で説明したように, \(y_3 = y_1′, y_4 = y_2’\) のようにして 4 元連立方程式として扱います.

プログラム例を示します.

Const Ndata = 19, RowR = 5, ColR = 1
Dim Neval As Long

Sub F2(N As Long, T As Double, Y() As Double, Yp() As Double)
    Dim R As Double
    R = (Y(0) ^ 2 + Y(1) ^ 2) ^ (3 / 2)
    Yp(0) = Y(2)
    Yp(1) = Y(3)
    Yp(2) = -Y(0) / R
    Yp(3) = -Y(1) / R
    Neval = Neval + 1
End Sub

Sub Start_2()
    Const N = 4
    Dim Y(N - 1) As Double, T As Double, Tout As Double, Tend As Double
    Dim RTol(0) As Double, ATol(0) As Double
    Dim Mode As Long, Info As Long, I As Long
    RTol(0) = 0.00000001 '**1e-8
    ATol(0) = RTol(0)
    Mode = 2
    T = Cells(RowR, ColR)
    Y(0) = Cells(RowR, ColR + 1)
    Y(1) = Cells(RowR, ColR + 2)
    Y(2) = Cells(RowR, ColR + 3)
    Y(3) = Cells(RowR, ColR + 4)
    Tend = Cells(RowR + Ndata, ColR)
    Info = 0
    For I = 1 To Ndata
        Tout = Cells(RowR + I, ColR)
        Neval = 0
        Call Derkfa(N, AddressOf F2, T, Y(), Tout, Tend, RTol(), ATol(), Mode, Info)
        If Info <> 0 And Info <> Mode Then
            Cells(RowR + I, ColR + 2) = "Error: " + Str(Info)
            Exit For
        End If
        Cells(RowR + I, ColR + 1) = Y(0)
        Cells(RowR + I, ColR + 2) = Y(1)
        Cells(RowR + I, ColR + 3) = Y(2)
        Cells(RowR + I, ColR + 4) = Y(3)
        Cells(RowR + I, ColR + 5) = Neval
    Next
End Sub

連立ではない単一の常微分方程式(例題 1)の場合と違うのは配列 Y() と Yp() に複数(この場合は 4 つ)の式の値を設定することだけです.

このプログラムを実行すると, 次の結果が得られました.

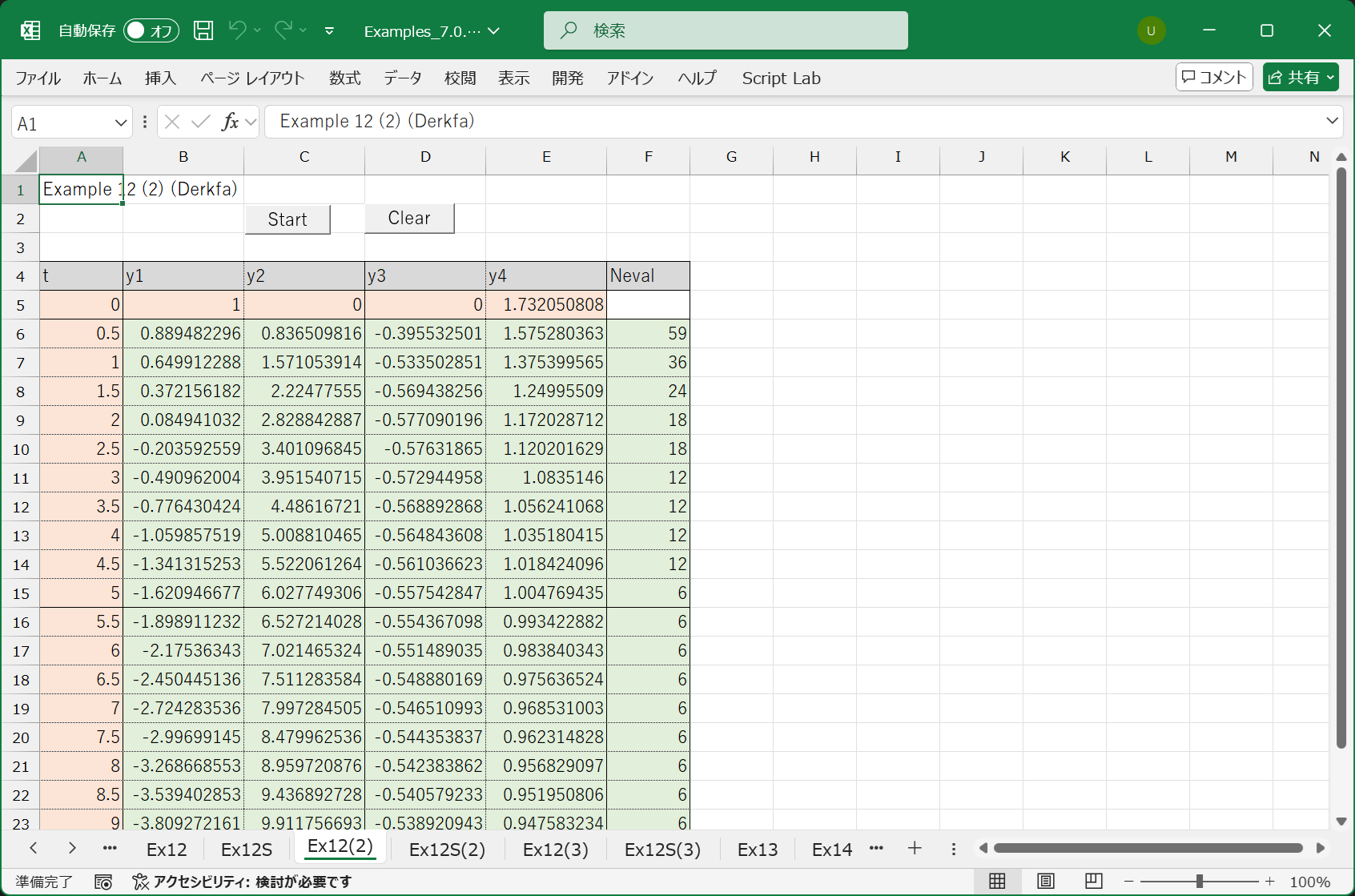
12.3.2.2 VBA プログラムを使用した解き方 (2)

例題 2 には 1 階の項が現れないので Dopn43 を使うことができ, 2 元連立方程式のまま扱うことができます. プログラム例を示します.

Const Ndata = 19, RowR = 5, ColR = 1
Dim Neval As Long

Sub F3(N As Long, T As Double, Y() As Double, Yp2() As Double)
    Dim R As Double
    R = (Y(0) ^ 2 + Y(1) ^ 2) ^ (3 / 2)
    Yp2(0) = -Y(0) / R
    Yp2(1) = -Y(1) / R
    Neval = Neval + 1
End Sub

Sub Start_3()
    Const N = 2
    Dim T As Double, Y(N - 1) As Double, Yp(N - 1) As Double, Tout As Double, Tend As Double
    Dim RTol(0) As Double, ATol(0) As Double
    Dim Mode As Long, Info As Long, I As Long
    RTol(0) = 0.00000001 '1.0e-8
    ATol(0) = RTol(0)
    Mode = 2
    T = Cells(RowR, ColR)
    Y(0) = Cells(RowR, ColR + 1)
    Y(1) = Cells(RowR, ColR + 2)
    Yp(0) = Cells(RowR, ColR + 3)
    Yp(1) = Cells(RowR, ColR + 4)
    Tend = Cells(RowR + Ndata, ColR)
    Tend = 12
    Info = 0
    For I = 1 To Ndata
        Tout = Cells(RowR + I, ColR)
        Neval = 0
        Call Dopn43(N, AddressOf F3, T, Y(), Yp(), Tout, Tend, RTol(), ATol(), Mode, Info)
        If Info <> 0 And Info <> Mode Then
            Cells(RowR + I, ColR + 2) = "Error: " + Str(Info)
            Exit For
        End If
        Cells(RowR + I, ColR + 1) = Y(0)
        Cells(RowR + I, ColR + 2) = Y(1)
        Cells(RowR + I, ColR + 3) = Yp(0)
        Cells(RowR + I, ColR + 4) = Yp(1)
        Cells(RowR + I, ColR + 5) = Neval
    Next
End Sub

Dopn43 は階数が異なること以外, Derkfa と同じ使い方になります.

このプログラムを実行すると, 次の結果が得られました.

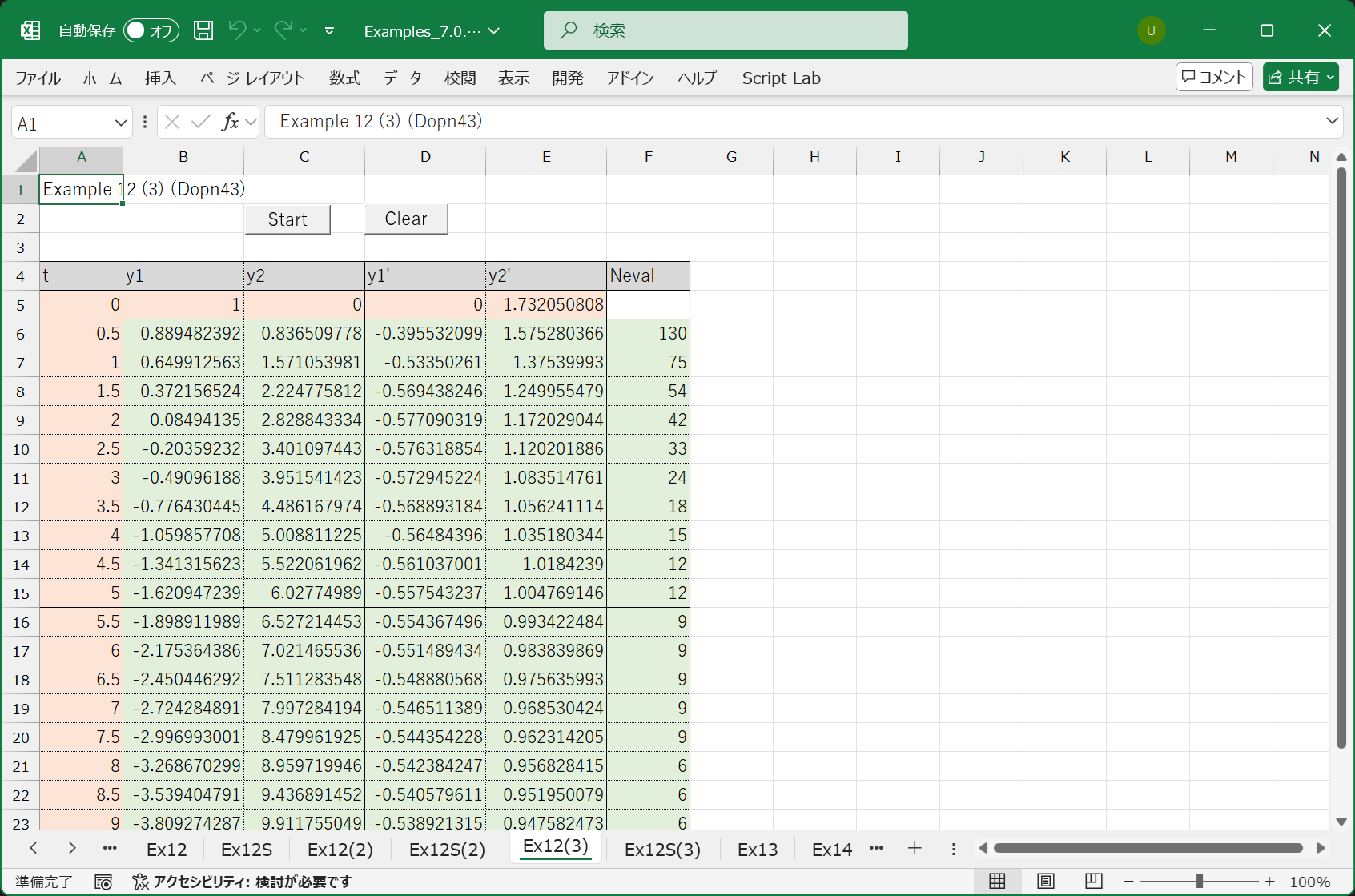
12.3.2.3 ソルバーを使用した解き方

XLPack ソルバーアドインの「2 階常微分方程式」を使って解くこともできます.

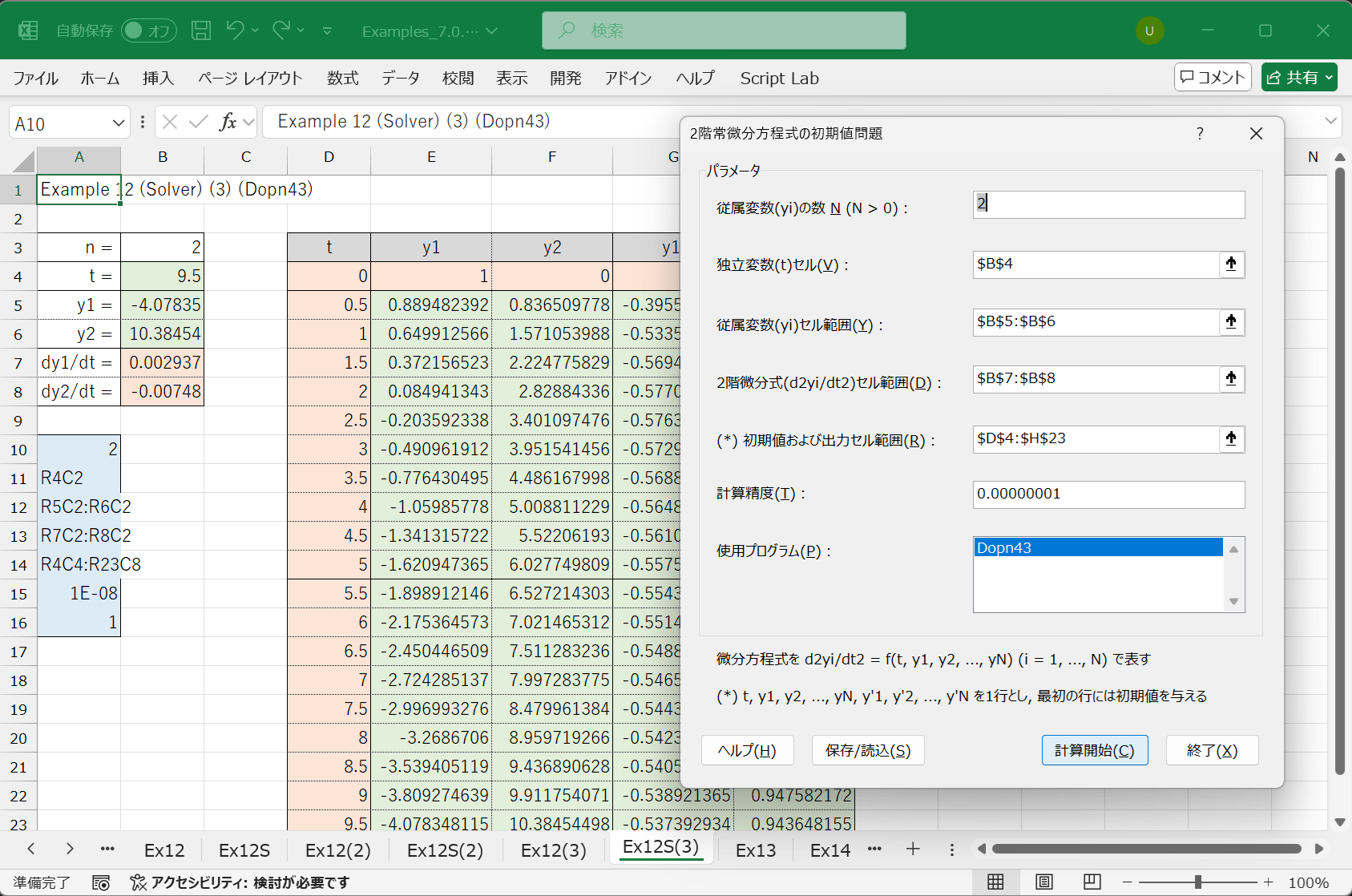
ソルバーについては こちら も参照ください.

なお, ダウンロードできる例題ワークシートにはソルバーアドインの「1 階常微分方程式」を使った例も入っています.