4. 線形最小二乗法
注 – 例題ワークシートをダウンロードすることができます. 1. 例題ワークシートの入手と使用方法 をご覧ください.
線形最小二乗問題の XLPack による解き方の例を説明します.
例題: 多項式近似
次のデータは, NIST(アメリカ国立標準技術研究所)のホームページ(http://www.itl.nist.gov/div898/strd/lls/data/Norris.shtml)に掲載されているテストデータです.
Data: y x
0.1 0.2
338.8 337.4
118.1 118.2
888.0 884.6
9.2 10.1
228.1 226.5
668.5 666.3
998.5 996.3
449.1 448.6
778.9 777.0
559.2 558.2
0.3 0.4
0.1 0.6
778.1 775.5
668.8 666.9
339.3 338.0
448.9 447.5
10.8 11.6
557.7 556.0
228.3 228.1
998.0 995.8
888.8 887.6
119.6 120.2
0.3 0.3
0.6 0.3
557.6 556.8
339.3 339.1
888.0 887.2
998.5 999.0
778.9 779.0
10.2 11.1
117.6 118.3
228.9 229.2
668.4 669.1
449.2 448.9
0.2 0.5
これを1次多項式(直線)
f(x) ≅ c1 + c2x
により近似します.
以下, ワークシート関数 WDgels と VBA サブルーチン Dgels を使った2種類の解き方を説明します.
ワークシート関数を使用した解き方
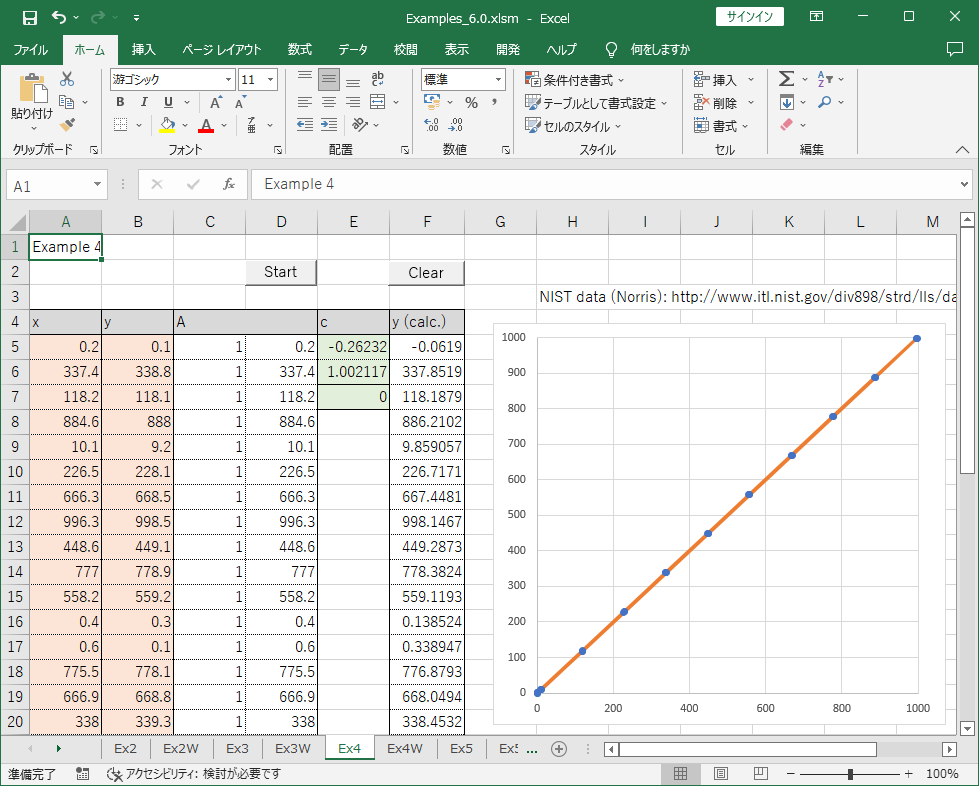
まず, ワークシートの適当な場所にデータを入力します(オレンジ色のセル). そして, 係数行列 A (Aij = φj(xi) (i = 1~m, j = 1~n)) を作ります(この場合は, Ai1 = 1, Ai2 = xi となるような式を入れておきります). 次に, 求めるパラメータ c およびその他の結果を入れる n+2 個のセルを選択してワークシート関数 WDgels を入力します(緑色のセル).
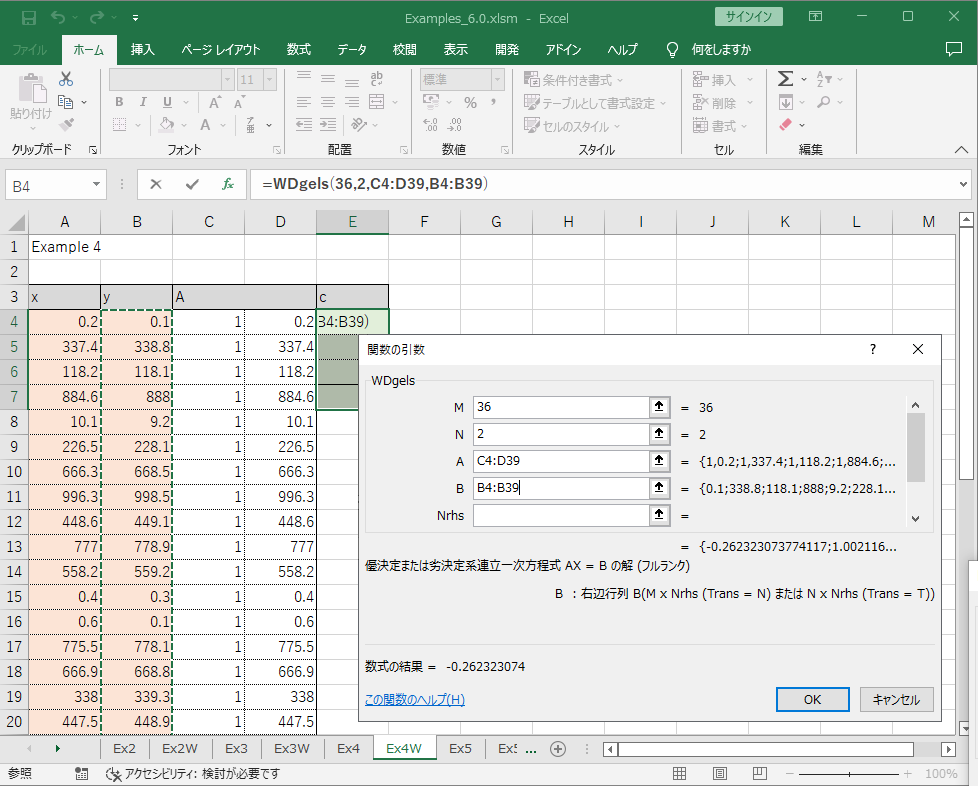
WDgels の必要なパラメータは, Trans, Cov, M, N, A, B, Nrhs です. Trans = “N” ならば Ax = b を解き, Trans = “T” ならば (A^T)x = b を解きます. Cov = “N” ならば分散共分散行列を計算しません. Cov = “D” ならば分散(分散共分散行列の対角要素)を計算します. Cov = “C” ならば分散共分散行列を計算します. M はデータ数, N はパラメータ数(この例では 2), A は行列 A のセル範囲, B は右辺ベクトル(= ベクトル y)のセル範囲です. 右辺ベクトルは通常は 1 本ですが, 複数本入力することもでき, Nrhs にはその本数を入力します. Nrhs は入力を省略することができ, その場合は 1 とみなされます.
入力が終了したら Ctrl + Shift + Enter を押すと結果が得られます. ここでは, データを丸で, 計算値を直線で表すグラフも作成してみました.

2つのパラメータが求められました(c1 = -0.26232, c2 = 1.002117). これらは, NIST の値とぴったり一致しています.
VBAプログラムを使用した解き方
上と同じ例を VBA プログラムにより解いてみます. VBA サブルーチン Dgels を使ったプログラム例を示します.
Sub Start()
Const MMax = 100, NMax = 5
Dim M As Long, N As Long
Dim A(MMax, NMax) As Double, B(MMax) As Double
Dim Info As Long, I As Long, J As Long
'--- Input data
M = 36: N = 2
For I = 0 To M - 1
For J = 0 To N - 1
A(I, J) = Cells(5 + I, 3 + J)
Next
B(I) = Cells(5 + I, 2)
Next
'--- Compute least squares solution
Call Dgels("N", M, N, A(), B(), Info)
'--- Output result
For J = 0 To N - 1
Cells(5 + J, 5) = B(J)
Next
Cells(7, 5) = Info
End Sub所定の位置にデータを入力し, マクロ Start を実行すると次のように上と同じ結果が得られます. ワークシート関数を使用したときと異なり, 係数行列 A と右辺ベクトル b の値を入力しただけでは結果が得られず, VBA プログラムを実行してやる必要があります.