7. 非線形方程式 (1 変数)

7.1 概要

一般の 1 変数関数 f(x) の実数のゼロ点を求める問題を考えます.
\[
f(x) = 0
\] \(f(x)\) が多項式で表される場合は代数方程式と呼ばれ, それに特化した解法が用いられます(6 章を参照).

そうでない場合は非線形方程式(あるいは, 超越方程式)と呼ばれます. ここでは実数解が存在するものとします. 解析的に逆関数が求められない限りは, 適当な初期値を与えて反復法によって近似解を求めることになります.

7.2 非線形方程式 (1 変数) の解法

代表的な解法はニュートン法です. 収束が速く, 数値計算ではこれをベースにした解法が多く使われています. 他に, 安定した解法としてゼロ点を含む区間を縮小していく二分法が使われます.

7.2.1 ニュートン法

\(f(x)\) を第 k 近似 \(x_k\) のまわりでテイラー展開すると次のようになります.
\[
f(x) = f(x_k) + f'(x_k)(x – x_k) + (1/2)f”(x_k)(x – x_k)^2 + \dots
\] ここで, 右辺第 2 項までで近似し (2 次以上の項を 0 とみなし), \(f(x) = 0\) とすると次式が得られます.
\[
x = x_k – f(x_k)/f'(x_k)
\] この \(x\) を第 k + 1 近似 \(x_{k+1}\) とすると次のニュートン法の反復式が得られます.
\[
\begin{align}
& d_k = -f(x_k)/f'(x_k) \\
& x_{k+1} = x_k + d_k \\
\end{align}
\] 反復は, 適当な初期近似 \(x_0\) から開始し, \(|d_k|\) が十分に小さくなったら収束とみなし終了します.

式の誤差は \(d_k\) の二乗のオーダーになり, この解法は 2 次収束するといいます.

この解法の幾何的解釈は次のとおりです.

\(x_0\) から始めてその点における接線が \(x\) 軸と交わる点を \(x_1\) とします. 微分値 \(f'(x_0)\) は接線の傾きを表すので, それを使って交点 \(x_1\) を求めることができます.

同様に \(x_2, x_3, \dots\) というように繰り返し次の点を求めていくと, 急速に解に近づいていくことがわかります.

この解法は収束が速いためよく使われます. ただし, 微分値 \(f'(x)\) の計算が難しい場合には適用できないことがあります.

また, 解に十分近く関数が滑らかであるとみなせる領域の初期値を与える必要があります. 初期値が悪いために失敗する例は次のようなものです.

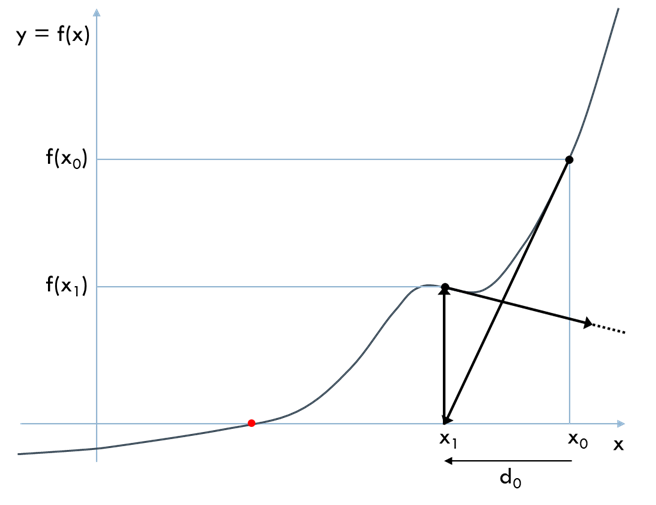
この例では 2 回目の反復において発散して (想定外の \(x\) に跳んで) います. 結果的には, オーバーフローを引き起こしたり無限ループに陥ったりします.

7.2.2 二分法

初期値として 2 つの点 \(a\) と \(b\) を与えます. それぞれにおける関数値は \(f(a)\) と \(f(b)\) です. 区間 \([a, b]\) には解が 1 つだけ入っていなければなりません. 従って, \(f(a)\) の符号と \(f(b)\) の符号は反対でなければなりません.

中点 \(c = (a + b)/2\) で関数値 \(f(c)\) を計算します.

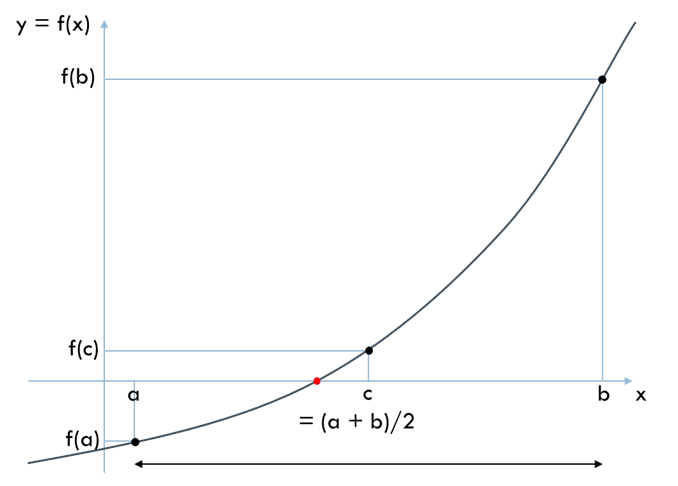
\(f(c)\) の符号と \(f(a)\) の符号が同じならば, \(c\) を新しい \(a\) とします. そうでなければ, \(c\) を新しい \(b\) とします. そして新しい \(c = (a + b)/2\) を求め, 繰り返します.

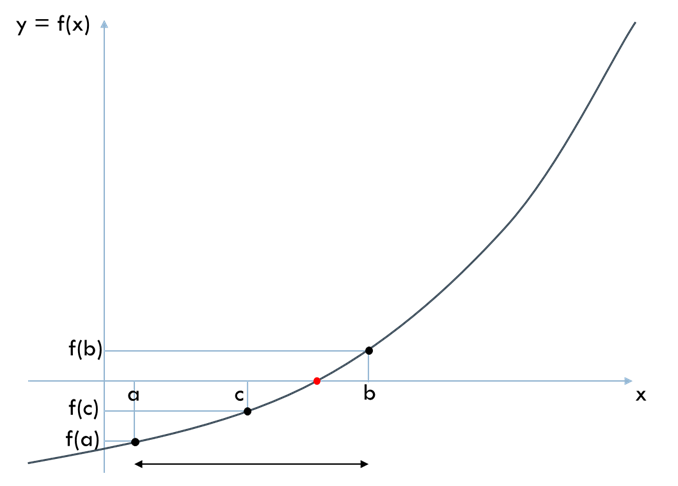
このようにして反復のたびに区間の幅を半分にしていく解法を二分法といいます. 区間の幅が十分に小さくなったら反復を終了します.

この解法は, 収束は速くありませんが, 解をはさむ区間がわかってさえいれば確実に収束する特長があります. また, 微分値の計算が不要なのもメリットとなります.

7.3 XLPack を使った 1 変数非線形方程式の解き方

VBA サブルーチン Dfzero は解をはさむ区間を与えると二分法よりも高速に解を見つけるプログラムです. 反復において \(a, b, c\) の 3 点を使って補間を行いゼロ点を推定します. それが妥当であれば採用し, そうでなければ二分法の反復を行います. 全体として二分法よりも速く収束することになります. Dfzero は XLPack ソルバーから使うこともできます.

例題

次の方程式を解く.
\[
f(x) = x^3 – 2x – 5 = 0
\] \(f(x)\) の形を確認するためにグラフを描いてみます.

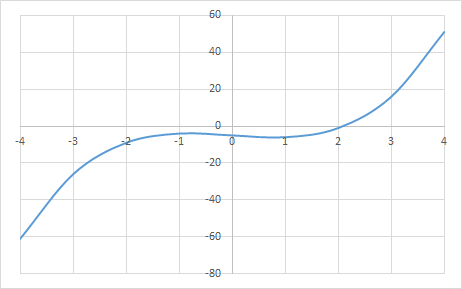
ゼロ点は \(x = 2\) 付近にあることがわかるので, ゼロ点をはさむ区間として \([1, 3]\) を採用することにします.

7.3.1 VBA プログラムを使用した解き方 (1)

Dfzero を使ったプログラム例を示します.

Function F(X As Double) As Double
    F = X ^ 3 - 2 * X - 5
End Function

Sub Start()
    Dim Ax As Double, Bx As Double, Rx As Double, Re As Double, Ae As Double, Info As Long
    '--- Input data
    Ax = 1
    Bx = 3
    Rx = Ax
    Re = 0.000000000000001 '1e-15
    Ae = Re
    '--- Compute zero of equation
    Call Dfzero(AddressOf F, Ax, Bx, Rx, Re, Ae, Info)
    '--- Output zero
    MsgBox Str(Ax) & " (Info = " & Str(Info) & ")"
End Sub

目的関数を外部関数として用意し, 区間と要求精度を指定して呼び出します.

Dfzero には確実にゼロ点をはさむ区間を与えるように注意が必要です. なお, 与えられた区間に 2 つ以上のゼロ点が含まれている場合, どの点に収束するかはわかりません.

このプログラムを実行すると, \(x = 2.0945514815\) が得られます.

7.3.2 VBA プログラムを使用した解き方 (2)

リバースコミュニケーション版 (RCI) の Dfzero_r を使ったプログラム例を示します.

Sub Start()
    Dim Ax As Double, Bx As Double, Rx As Double, Re As Double, Ae As Double, Info As Long
    Dim XX As Double, YY As Double, IRev As Long
    '--- Input data
    Ax = 1
    Bx = 3
    Rx = Ax
    Re = 0.000000000000001 '1e-15
    Ae = Re
    '--- Compute zero of equation
    IRev = 0
    Do
        Call Dfzero_r(Ax, Bx, Rx, Re, Ae, Info, XX, YY, IRev)
        If IRev <> 0 Then YY = XX ^ 3 - 2 * XX - 5
    Loop While IRev <> 0
    '--- Output zero
    MsgBox Str(Ax) & " (Info = " & Str(Info) & ")"
End Sub

目的関数を外部関数として与えるのではなく, IRev = 1のときに XX の値を使って関数値を計算し YY に入れて再度 Dfzero_r を呼び出します. RCI の詳細についてはこちらを参照してください.

このプログラムを実行すると上と同じ結果が得られます.

7.3.3 ソルバーを使用した解き方

XLPackソルバーアドインの「１変数非線形方程式」を使って解くこともできます. B7セルに数式 (=B6^3-2*B6-5) が入力されています.

ソルバーについてはこちらも参照ください.

公開日: 2025/03/31 (更新日: 2025/08/19)