9. 非線形最適化 (1 変数)

9.1 概要

1 変数の非線形関数 (一般関数) の最小点 (符号を逆にすれば最大点) を求める問題を考えます.
\[
min f(x)
\] ここで, 対象とする領域内では 1 つの最小点しか持たないものとします. すなわち, 目的とする最小点の近傍だけに着目することにします. これを局所的最適化あるいは局所的最小点を求めるなどといいます.

9.2 非線形最適化の解法 (1 変数)

9.2.1 黄金分割探索法

初期値として \(a\) と \(b\) を与えます. 関数値は \(f(a)\) と \(f(b)\) です. 最小点 1 つが区間 \([a, b]\) に入っていなければなりません.

\(r = (\sqrt{5} – 1)/2 (\simeq 0.618)\) は黄金比(の逆数)と呼ばれる値です. これについて \(r^2 = 1 – r\) が成り立ちます.

区間幅\(\times (1 – r)\) および 区間幅\(\times r\) の点を \(c\) および \(d\) とします. すなわち, \(c = a + (b – a)(1 – r), d = a + (b – a)r\) とします. そして, 関数値 \(f(c)\) および \(f(d)\) を計算します.

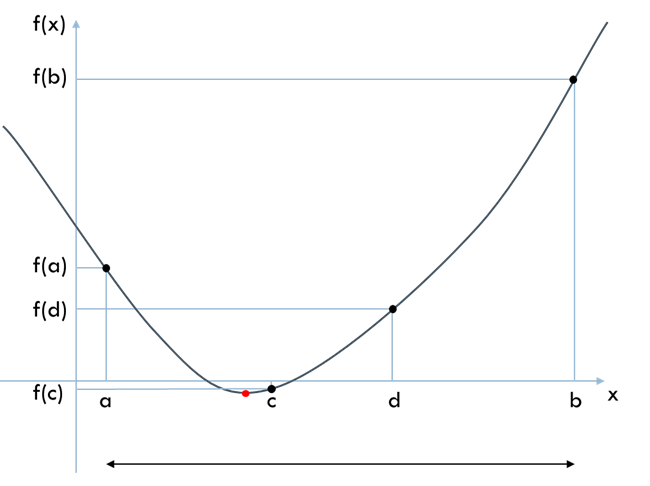
\(f(c) < f(d)\) ならば, \(d\) を新しい \(b\) として区間を縮小します. そうすると, \(新区間幅 = 旧区間幅 \times r\) となります. 新しい \(c\) と \(d\) は \[ \begin{align} & 新c: 新区間幅 \times (1 - r) = 旧区間幅 \times (1 - r)r \space の点 \\ & 新d: 新区間幅 \times r = 旧区間幅 \times r^2 = 旧区間幅 \times (1- r) \space の点 \end{align} \] となり, \(新d = 旧c\) となっています. すなわち, 新区間では \(新c\) での関数値だけを計算すればよいことになります. \(f(c) > f(d)\) ならば, \(c\) を新しい \(a\) として区間を縮小し, 同様に \(新d\) での関数値だけを計算すればよくなります.

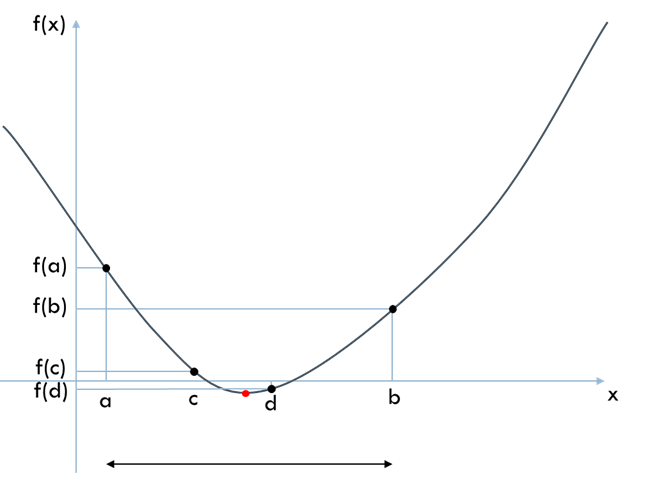
以上を繰り返して区間幅が十分に小さくなったら終了します.

この方法は黄金分割探索法と呼ばれます. 1 回の繰り返しで区間幅は約 0.618 倍に縮小するので, 似たような解法である非線形方程式の二分法(0.5 倍)より少し収束が遅くなります.

9.3 XLPack を使った 1 変数関数の非線形最適化の解き方

VBA サブルーチン Dfmin は最小点を含む区間を与えると黄金分割探索より速く最小点を見つけるプログラムです. 非線形方程式の Dfzero と同じように補間と組み合わせることにより黄金分割探索より速く収束します. Dfmin は XLPack ソルバーから使うこともできます.

例題

次の関数の \(x = 1\) 付近の最小点を求める.
\[
f(x) = x^3 – 2x – 5
\] \(f(x)\) の形は次のとおりで, 大域的には最小点はない (\(-\infty\) に発散する) ものの, \(x = 1\) 付近に局所的な最小点があるのがわかります.

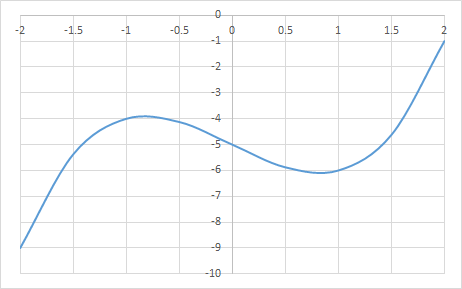
9.3.1 VBA プログラムを使用した解き方 (1)

Dfmin を使った VBA プログラム例を示します.

Function F(X As Double) As Double
    F = X ^ 3 - 2 * X - 5
End Function

Sub Start()
    Dim Ax As Double, Bx As Double, Tol As Double, X As Double
    '--- Input data
    Ax = 0
    Bx = 1.5
    Tol = 0.000000000000001 '1e-15
    '--- Compute min. point of equation
    Call Dfmin(Ax, Bx, AddressOf F, Tol, X)
    '--- Output min. point
    MsgBox X
End Sub

Dfmin は, 与えられた区間 \([Ax, Bx]\) で局所的な最小点が 1 つ挟まれているものとして, その最小点を求めます. この場合, 最小点は 1 付近にあるので, \(Ax = 0, Bx = 1.5\) としました.

このプログラムを実行すると, \(x = 0.81650\) が求められます.

9.3.2 VBA プログラムを使用した解き方 (2)

リバースコミュニケーション版 (RCI) の Dfmin_r を使ったプログラム例を示します.

Sub Start()
    Dim Ax As Double, Bx As Double, Tol As Double, X As Double
    Dim XX As Double, YY As Double, IRev As Long
    '--- Input data
    Ax = 0
    Bx = 1.5
    Tol = 0.000000000000001 '1e-15
    '--- Compute min. point of equation
    IRev = 0
    Do
        Call Dfmin_r(Ax, Bx, Tol, XX, YY, IRev)
        If IRev <> 0 Then YY = XX ^ 3 - 2 * XX - 5
    Loop While IRev <> 0
    X = XX
    '--- Output min. point
    MsgBox X
End Sub

目的関数を外部関数として与えるのではなく, IRev = 1 のときに XX の値を使って関数値を計算し YY に入れて再度 Dfmin_r を呼び出します. RCI の詳細については こちら を参照してください.

このプログラムを実行すると上と同じ結果が得られます.

9.3.3 ソルバーを使用した解き方

XLPackソルバーアドインの「１変数非線形最適化」を使って解くこともできます. B7セルに数式 (=B6^3-2*B6-5) が入力されています.

ソルバーについては こちら も参照ください.