11. 数値積分

11.1 概要

\(f(x)\) は区間 \([a, b]\) 上で定義された関数とし, その定積分
\[
I = \int_a^b f(x) dx
\] を数値的に求めます.

大きく 2 種類の数値積分プログラムがあります. 1 つは関数入力タイプで, 被積分関数値が要求に応じて区間内の任意の点で計算できる場合に使われます. もう 1 つはデータ入力タイプで, 区間を包含するいくつかの点のみでの被積分関数値が知られている場合に使われます.

11.2 数値積分の解法

例題

次の定積分を求める.
\[
I = \int_0^4 1/(x + 1) dx
\] 被積分関数 \(1/(x + 1)\) の関数形は次のようになります.

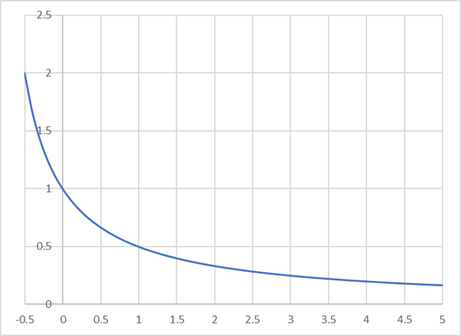
この関数は解析的に積分関数を求めることができて \(ln(x + 1) + C\) となります(\(C\) は積分定数). \(a = 0, b = 4\) の場合には \(I = 1.609437912\) となります.

11.2.1 関数入力タイプ

積分の近似値を求めるためには多くの公式が知られています. 例えば, 台形公式やシンプソン公式です.

11.2.1.1 台形公式

\(x = a\) と \(x = b\) の間を直線で補間して台形の面積で近似します.
\[
I = (f(a) + f(b))(b – a)/2
\] 例題に適用すると次のようになります.

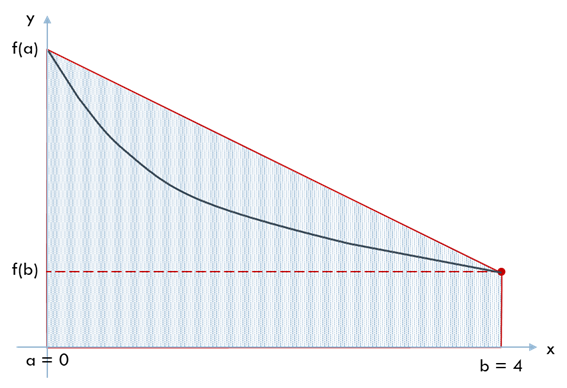
\(I = 2.4000\) (誤差 49.1%) となりました.

11.2.1.2 シンプソン公式

\(x = a\) と \(x = b\) の間のもう 1 点(通常は中点)でも関数値を求め, 3 点を二次曲線で補間してその積分値で近似します.
\[
I = (f(a) + 4f((a + b)/2) + f(b))(b – a)/6
\] 例題に適用すると次のようになります.

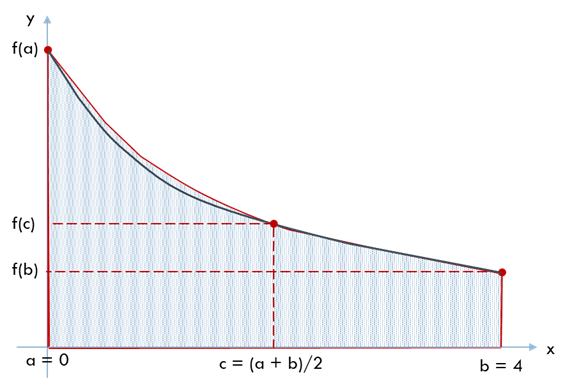
\(I = 1.6889\) (誤差 4.94%) と台形公式よりかなり良くなりました. ただし, \(f(x)\) の計算回数は 3 回となり, 台形公式の 2 回より多くなります.

数値積分の計算量 (1/計算速度) はおおむね \(f(x)\) の計算回数に依存すると考えることができますので, この場合はシンプソン公式では台形公式に比べて 1.5 倍の計算量が必要な代わりに 10 倍以上の精度が得られるといえます.

11.2.1.3 複合公式

精度を上げるために積分区間をいくつかの部分区間に分割してそれぞれに台形公式やシンプソン公式を適用する方法が考えられます. 部分区間の幅は任意ですがここでは均等に分割して \(h\) と表すことにします.

区間 \([a, b]\) を \(n\) 個の部分区間 \([x_i, x_{i+1}] (i = 1 \sim n)\) に分割して定積分を次のように表します.
\[
I = \sum_{i=1}^n I_i
\] ただし,
\[
I_i = \int_{x_i}^{x_{i+1}}f(x) dx \\
x_1 = a, x_{n+1} = b, h = (b – a)/n
\] 部分区間に台形公式を適用すると次のようになります.
\[
I_i = h(f(x_i + f(x_{i+1}))/2
\] これを複合台形公式といいます. ただし, 単に台形公式といえば複合台形公式を指すことがよくあります.

例題の積分区間を 4 分割 \((m = 4)\) して台形公式を適用すると次のようになります.

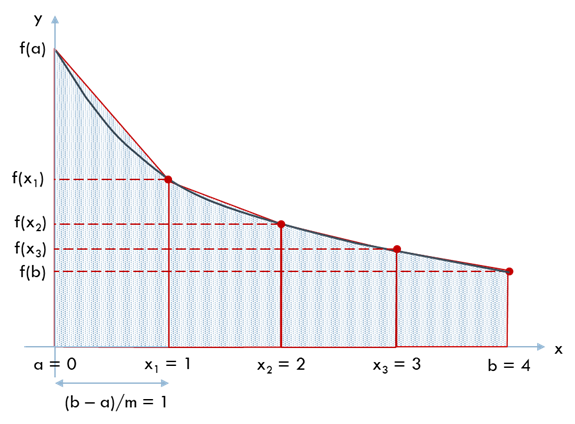
\(I = 1.6833\) (誤差 4.59%) と分割前の 49.1% より約 10 倍良くなりました. \(f(x)\) の計算回数は 5 回と 2.5 倍になりました.

同様に部分区間にシンプソン公式を適用すると次のようになります.
\[
I_i = h(f(x_i + 4f((x_i + x_{i+1})/2) + f(x_{i+1}))/6
\] これを複合シンプソン公式といいます. これも, 単にシンプソン公式と呼ぶことがあります.

\(f(x)\) の計算回数が複合台形公式の場合と同じく 5 回になるように例題を 2 分割 \((m = 2)\) して適用してみると次のようになります.

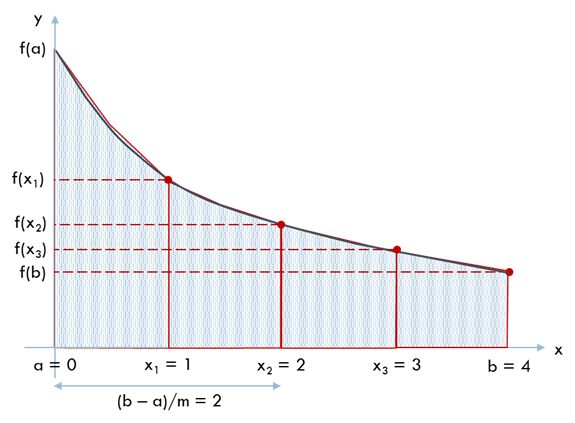
\(I = 1.6222\) (誤差 0.79%) と分割前の 4.94% より 5 倍程度良くなりました. \(f(x)\) の計算回数が同じ (分割数が半分) 場合でもシンプソン公式は台形公式よりかなり精度が良いことがわかります.

11.2.1.4 ガウス公式

シンプソン公式よりもさらに精度の良い方法としてガウス公式 (ガウス・ルジャンドル公式ともいう) があります.

ガウス公式は積分区間を直交多項式の 1 つであるルジャンドル多項式で補間する方法です.

この公式では \(f(x)\) を計算する点 \(x_i\) はルジャンドル多項式のゼロ点に固定されており, 各点での重み \(w_i\) を使って積分値は次のように表されます.
\[
I = ((b – a)/2)\sum_{i=1}^n w_if((a + b)/2 + ((b – a)/2)x_i)
\] \(x_i\) と \(w_i\) は教科書や公式集の数表に載っています. ちなみに \(n = 2 と 3\) の場合には次のようになります. それぞれ, 2 点ガウス公式, 3 点ガウス公式ということもあります.
\[
\begin{array}{ccccccc}
n & x1 & x2 & x3 & w1 & w2 & w3 \\ \hline
2 & -\sqrt{1/3} & \sqrt{1/3)} & – & 1 & 1 & – \\
3 & -\sqrt{3/5} & 0 & \sqrt{3/5} & 5/9 & 8/9 & 5/9 \\
\hline
\end{array}
\] \(x_i\) には積分区間の両端 \(a\) と \(b\) が含まれません.

\(n = 2\) のガウス公式を例題に適用すると次のようになります.

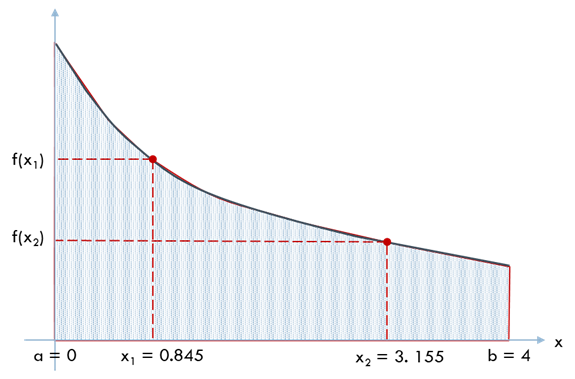
\(f(x)\) の計算回数は 2 回で, 誤差は 2.75% になりました.

\(n = 3\) のガウス公式を例題に適用すると次のようになります.

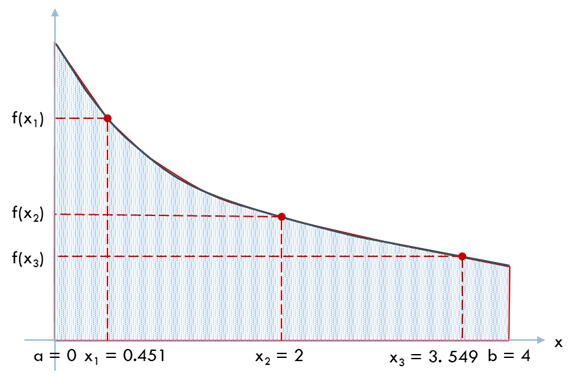
\(f(x)\) の計算回数は 3 回で, 誤差は 0.42% になりました.

ガウス公式は台形公式やシンプソン公式に比べて非常に精度がよいことがわかります. ちなみに, \(n = 4, 5\) で計算してみると誤差はそれぞれ 0.063%, 0.009% となりました.

ガウス公式の場合には, 精度を上げるためには \(n\) を大きくしていくか, 積分区間を部分区間に分割してそれぞれに公式を適用するようにします.

11.2.1.5 適応求積ルーチン

得られた積分値の誤差が推定できたとすると, 必要な精度を満たすように部分区間の数を増減させるなどして自動的に計算量を最適化 (要求精度を満たすが計算量をできるだけ少なくすること) できます. このようなプログラムを適応求積ルーチンといいます.

誤差を推定するためには, 例えば部分区間の数を変えて計算し結果を比較する方法などが考えられます. 台形公式やシンプソン公式で等間隔の部分区間に分割することした場合, 分割数が倍 (部分区間の幅が半分) になったときに半分の点では \(f(x)\) の計算済の結果を再利用できるため計算量を減らすことができます.

これに対して, ガウス公式の場合には \(n\) を変えると全部の点で \(f(x)\) の計算をし直す必要があり, 計算効率が良くありません. そこで, 1 つの公式で \(n\) が異なる 2 つの値を得ることができるガウス・クロンロッド公式が提案されました. これは次のようなものです.
\[
I = ((b – a)/2)(\sum_{i=1}^n a_if((a + b)/2 + ((b – a)/2)x_i) + \sum_{j=1}^{n+1} b_jf((a + b)/2 + ((b – a)/2)y_j))
\] ここで, \(a_i\) と \(b_j\) はガウス・クロンロッド公式の係数です. 始点・終点を表す \(a, b\) とは別のものです.

\(x_i\) はガウス公式と同じものです. したがって, ガウス公式の \(w_i\) と組み合わせると \(n\) 点ガウス公式を使った積分値 (\(G_n\) と表す) を求めることができます. なお, \(a_i\) と \(w_i\) の値は異なります.

全体では \(2n + 1\) 点ガウス・クロンロッド公式を使った積分値 (\(K_{2n+1}\) と表す) を求めることができます.

\(K_{2n+1}\) は \(f(x)\) の計算回数が同じ \(G_{2n+1}\) よりは精度が悪くなります. つまり, ガウス・クロンロッド公式は, ガウス公式よりはやや精度が落ちる代わりに誤差推定機能を追加したものといえます.

\(n = 2\) の場合 (5 点ガウス・クロンロッド公式) の係数は次のようになります.
\[
\begin{array}{cccc}
\hline
x_i & -0.5773502691896258 & 0.5773502691896258 \\
a_i & 0.4909090909090909 & 0.4909090909090909 \\
y_j & -0.9258200997725515 & 0 & 0.9258200997725515 \\
b_j & 0.1979797979797980 & 0.6222222222222222 & 0.1979797979797980 \\
\hline
\end{array}
\] 求められた \(G_n\) と \(K_{2n+1}\) から誤差を推定することができます.

5 点ガウス・クロンロッド公式を使用して例題の計算を行うと誤差 0.012% になりました. これは 4 点ガウス公式と 5 点ガウス公式の中間の精度という結果でした.

現在では数値積分には精度をある程度保証できるように適応求積ルーチンを使うのが一般的になっています. 特に各部分区間にガウス・クロンロッド公式を適用して誤差を推定し, 各部分区間の幅を最適化して精度を保ったまま計算量を減らすようにしたプログラムがよく使われています.

11.2.2 データ入力タイプ

入力されたデータ点の補間を行い, その補間式の積分を計算することにより積分値を求めるものです.

多項式補間するものやスプライン補間するものなどがあります. 入力データにもよりますが, 一般的には高い精度が期待できるものではありません.

11.3 XLPack を使った数値積分の求め方

VBAサブルーチン Qk15 は分点固定 (15点) のガウス・クロンロッド公式による数値積分プログラムです. 15 回の関数呼び出しで積分値とその推定誤差を計算します. VBA サブルーチン Qag はガウス・クロンロッド公式による適応求積ルーチンです. 被積分関数が滑らかな場合には Qk15 で十分な精度が得られます. 被積分関数が滑らかでない場合や, 関数呼び出しが増えてでも所定の目的精度を得たい場合には, Qag を使うとよいでしょう.

積分範囲の片方あるいは両方が有限でない場合には VBA サブルーチン Qagi を使うことができます. これもガウス・クロンロッド公式による適応求積分ルーチンです. 半無限積分を有限区間 [0, 1] の積分に変換して計算します.

Qag および Qagi は XLPack ソルバーから使うこともできます.

3次スプライン補間係数を求める VBA サブルーチン Pchse あるいはワークシート関数 WPchse (「5. 補間法」参照) に VBA サブルーチン Pchia あるいはワークシート関数 WPchia を組み合わせることによりデータ入力タイプの数値積分プログラムとして使用できます.

以下, 上の例題を解く例を説明します.

11.3.1 VBA プログラムを使用した解き方 (関数入力) (1)

Qag および Qk15 を使ったプログラム例を示します.

Function F(X As Double) As Double
    F = 1 / (1 + X)
End Function

Sub Start()
    Dim A As Double, B As Double, S As Double, Info As Long
    Dim AbsErr As Double, Neval As Long
    '--- Input data
    A = Cells(4, 2): B = Cells(5, 2)
    '--- Compute integration by Qag
    Call Qag(AddressOf F, A, B, S, Info, AbsErr, Neval)
    Cells(11, 2) = Info
    If Info = 0 Then
        Cells(8, 2) = S
        Cells(9, 2) = AbsErr
        Cells(10, 2) = Neval
    End If
    '--- Compute integration by Qk15
    Call Qk15(AddressOf F, A, B, S, AbsErr)
    Cells(8, 3) = S
    Cells(9, 3) = AbsErr
End Sub

目的関数を外部関数として用意し, 区間と必要に応じて他のパラメータを指定して呼び出します.

このプログラムを実行すると, 次の結果が得られます.

Qag は, 被積分関数呼び出し 75 回 (内部で Qk15 を 5 回呼び出し) で推定誤差 \(7.38 \times 10^{-13}\) の結果が得られました. Qk15 は被積分関数呼び出し 15 回で推定誤差 \(2.07 \times 10^{-5}\) となりました. 推定誤差は安全方向に算出されており, 実際にはそれぞれ \(2.22 \times 10^{-16}, 1.20 \times 10^{-11}\) でした.

11.3.2 VBA プログラムを使用した解き方 (関数入力) (2)

リバースコミュニケーション版 (RCI) の Qag_r および Qk15_r を使ったプログラム例を示します.

Sub Start()
    Dim A As Double, B As Double, S As Double, Info As Long
    Dim AbsErr As Double, Neval As Long
    Dim XX As Double, YY As Double, IRev As Long
    '--- Input data
    A = Cells(4, 2): B = Cells(5, 2)
    '--- Compute integration by Qag_r
    IRev = 0
    Do
        Call Qag_r(A, B, S, Info, XX, YY, IRev, AbsErr, Neval)
        If IRev = 1 Then YY = 1 / (1 + XX ^ 2)
    Loop While IRev <> 0
    Cells(11, 2) = Info
    If Info = 0 Then
        Cells(8, 2) = S
        Cells(9, 2) = AbsErr
        Cells(10, 2) = Neval
    End If
    '--- Compute integration by Qk15_r
    IRev = 0
    Do
        Call Qk15_r(A, B, S, XX, YY, IRev, AbsErr)
        If IRev = 1 Then YY = 1 / (1 + XX ^ 2)
    Loop While IRev <> 0
    Cells(8, 3) = S
    Cells(9, 3) = AbsErr
End Sub

目的関数を外部関数として与えるのではなく, IRev = 1 のときに XX の値を使って関数値を計算し YY に入れて再度 Qag_r あるいは Qk15_r を呼び出します. RCI の詳細については こちら を参照してください.

このプログラムを実行すると上と同じ結果が得られます.

11.3.3 ワークシート関数を使用した解き方 (データ入力)

データ入力の数値積分ルーチンとして, スプライン補間による積分の求め方を説明します.

上と同じ例において, 関数形は不明で, \(x = 0, 0.5, 1, \dots, 4\) における関数値のみが与えられているものとします.
\[
\begin{array}{cccc}
\hline
x & f(x) \\ \hline
0 & 1 \\
0.5 & 0.666667 \\
1 & 0.5 \\
1.5 & 0.4 \\
2 & 0.333333 \\
2.5 & 0.285714 \\
3 & 0.25 \\
3.5 & 0.222222 \\
4 & 0.2 \\
\hline
\end{array}
\] まずは, WPchse 関数を使ってスプライン関数の係数を求めます(「5. 補間」を参照).

いったん係数が求められれば, WPchia 関数を使って積分値を計算することができます. WPchia の必要なパラメータは A, B, N, X, Y, D です. A と B は積分範囲(この例では 0 と 4). N はデータ数(この例では 9), X と Y は補間データのセル範囲です. D はスプライン係数のセル範囲です.

Enter を押すと, 1.61082… で, 9点のデータから3桁程度の精度で積分値を求めることができました.

注 – 例題ワークシートには VBA を使ったスプライン補間による積分例も入っています.

11.3.4 ソルバーを使用した解き方

XLPack ソルバーアドインの「数値積分 (有限区間)」を使って解くこともできます. B4セルに被積分関数式 (=1/(1+B3^2)) が入力されています.

ソルバーについては こちら も参照ください.