3. 固有値・固有ベクトル

注 – 例題ワークシートをダウンロードすることができます. 1. 例題ワークシートの入手と使用方法 をご覧ください.

対称行列の固有値問題の XLPack による解き方の例を説明します.

例題

次の対称行列の固有値と固有ベクトルを求める.

  
        ( 10 -3  5 )
    A = ( -3  2 -1 )
        (  5 -1  5 )

 
以下, ワークシート関数 WDsyev と VBA サブルーチン Dsyev を使った2種類の解き方を説明します. これらは, すべての固有値と対応する固有ベクトル, あるいは, すべての固有値だけを求めることができます.

ワークシート関数を使用した解き方

まず, ワークシートの適当な場所に対称行列 A のデータを入力します(オレンジ色のセル). そして, 解を入れる場所として(解の領域 + 1行のセル)を選択してワークシート関数 WDsyev を入力します(緑色のセル).

WDsyev の必要なパラメータは, Jobz, Uplo, N, A です. Jobz = “N” ならば固有値のみ求め, Jobz = “V” ならば固有値と固有ベクトルを求めます. Uplo = “U” ならば A の上三角部分を参照し, Uplo = “L” ならば A の下三角部分を参照します. N は要素数 (この例では 3), A は対称行列 A のセル範囲です.

ここでは対称行列 A のすべての要素の値を入力していますが, WDsyev は指定された上または下三角部分と対角要素しか使わないので, 残りの三角部分は入力しなくても構いません.

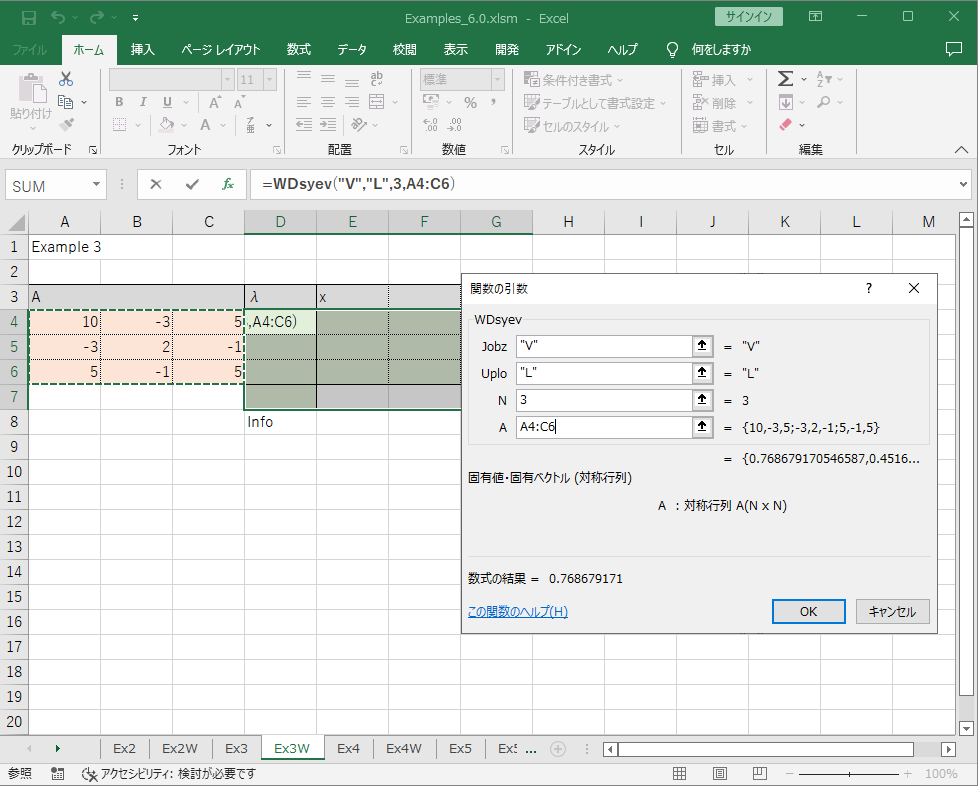
入力が終了したら Ctrl + Shift + Enter を押します.

これで, 3 つの固有値λとそれぞれに対応する固有ベクトル x (縦ベクトル) が求められました. 固有値の下に表示されている 0 はリターンコード(正常終了を示す)です.

VBA プログラムを使用した解き方

上と同じ例を VBA プログラムにより解いてみます. VBA サブルーチン Dsyev を使った VBA プログラム例を示します.

Sub Start()
    Const NMax = 10
    Dim N As Long, A(NMax, NMax) As Double, W(NMax) As Double
    Dim Info As Long, I As Long, J As Long
    '--- Input data
    N = 3
    For I = 0 To N - 1
        For J = 0 To N - 1
            A(I, J) = Cells(5 + I, 1 + J)
        Next
    Next
    '--- Compute eigenvalues and eigenvectors
    Call Dsyev("V", "L", N, A(), W(), Info)
    '--- Output result
    For I = 0 To N - 1
        For J = 0 To N - 1
            Cells(5 + I, 5 + J) = A(I, J)
        Next
        Cells(5 + I, 4) = W(I)
    Next
    Cells(8, 4) = Info
End Sub

所定の位置(下のオレンジ色のセル)に対称行列 A の値を入力し, マクロ Start としてプログラムを実行すると次の結果が得られます. ワークシート関数を使用したときと異なり, 行列 A の値を入力しただけでは結果が得られず, VBA プログラムを実行してやる必要があります.

なお, ここでは配列 A() に全要素を読み込むようにしていますが, Dsyev はワークシートの場合と同様に指定された上または下三角部分と対角要素しか使いません.